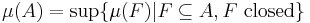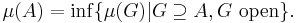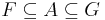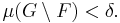Regular measure
In mathematics, a regular measure on a topological space is a measure for which every measurable set is "approximately open" and "approximately closed".
Contents |
Definition
Let (X, T) be a topological space and let Σ be a σ-algebra on X that contains the topology T (so that all open and closed sets are measurable sets, and Σ is at least as fine as the Borel σ-algebra on X). Let μ be a measure on (X, Σ). A measurable subset A of X is said to be μ-regular if
and
Alternatively, A is a μ-regular set if and only if, for every δ > 0, there exists a closed set F and an open set G such that
and
The two definitions are equivalent if 
is finite (otherwise, the second definition is stronger). If every measurable set is regular, then the measure μ is said to be a regular measure.
Some authors require the set F to be compact (not just closed).[1]
Examples
- Lebesgue measure on the real line is a regular measure: see the regularity theorem for Lebesgue measure.
- Any Borel probability measure on any metric space is a regular measure.
- The trivial measure, which assigns measure zero to every measurable subset, is a regular measure.
- A trivial example of a non-regular measure on the real line with its usual topology is the measure μ where
,
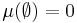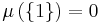, and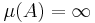
for any other set 
.
Notes
- ^ Dudley 1989, Sect. 7.1
References
- Billingsley, Patrick (1999). Convergence of Probability Measures. New York: John Wiley & Sons, Inc.. ISBN 0-471-19745-9.
- Parthasarathy, K. R. (2005). Probability measures on metric spaces. AMS Chelsea Publishing, Providence, RI. p. xii+276. ISBN 0-8218-3889-X. MR2169627 (See chapter 2)
- Dudley, R. M. (1989). Real Analysis and Probability. Chapman & Hall.